Znajomość częstości drgań własnych elementów maszyn i węzłów konstrukcyjnych hydrozespołów jako pomoc w rozpoznawaniu i nadzorowaniu ich stanu technicznego szczególnie w aspekcie remontu.

Artykuł prezentowany w ramach konferencji HYDROFORUM 2000

 2. Przykłady rozwiązania problemów wynikłych w związku z występowaniem drgań rezonansowych

  2.1.1. Ogólny stan dynamiczny i techniczny układu wirującego

   W 1994r. jedna z EW zwróciła się o: “ustalenie przyczyn urywania się opływki wirnika turbiny oraz podanie sposobu usunięcia tej przyczyny” [1].

• Przy obciąźeniu N = 0,4 MW  wartość “bicia” wału wynosi 2A = 1,14 mm,
• Przy obciąźeniu N = 2,0 MW  wartość “bicia” wału wynosi 2A = 1,33 mm,
• Przy obciąźeniu N = 4,0 MW  wartość “bicia” wału wynosi 2A = 1,46 mm,
• Przy obciąźeniu N = 6,0 MW  wartość “bicia” wału wynosi 2A = 1,45 mm,
• Przy obciąźeniu N = 8,0 MW  wartość “bicia” wału wynosi 2A = 1,59 mm,
• Przy obciąźeniu N = 10 MW  wartość “bicia” wału wynosi 2A =  1,29 mm,
• Przy obciąźeniu N = 12 MW  wartość “bicia” wału wynosi 2A =  1,27 mm,
• Przy obciąźeniu N = 14 MW  wartość “bicia” wału wynosi 2A =  1,17 mm. 

   Z powyźszego zestawienia wynika, źe gdy wzrasta napór na łopaty wirnika, występuje samo centrowanie wirnika w komorze, a szczeliny na obwodzie wirnika w komorze mają tendencję do wyrównywania swoich wartości. Wyrównanie szczelin pociąga za sobą spadek zawirowania strugi wody w stoźku wylotowym. Stąd wynika najspokojniejszy ruch wału przy obciąźeniu maksymalnym. Przy obciąźeniu minimalnym i maksymalnym, gdy ruch wirowy strugi jest najspokojniejszy kontakt wału z obudową łoźyska jest najmniejszy (po przeglądzie okazało się, ze łoźysko jest rozbite). Potwierdza to analiza przyśpieszeń drgań bezwzględnych obudowy łoźyska prowadzącego turbiny .
Z przebiegów drgań względnych wynika, źe oś wirnika porusza się równolegle do osi geometrycznej łoźysk, czyli bez ruchu stoźkowego charakterystycznego dla wahadłowego ruchu wału wokół środka masy wirnika. Z zaleźności geometrycznych wynika, źe jeźeli bicie wału w punkcie 4 wynosi 2A = 0,048 mm, a punkt 3 jest praktycznie w bezruchu (bicie wału w tym miejscu wynosi 2A = 0,003 mm) , to bicie wału w punkcie 6 powinno wynosić 2A = 0,081 mm, a faktycznie wynosi 2A = 0,04 mm. Moźna stwierdzić, źe występuje skrzywienie wału wirnika generatora. Potwierdziły to pomiary przeprowadzone przy pomocy poziomicy.
 Wypionowany w pochylonej komorze wirnika wał zachowuje się tak jak gdyby naruszona została nastawa zaleźności kombinatorowej. Naruszona zostaje równomierność strugi bezpośrednio za wirnikiem, co pociąga gwałtowny wzrost wibracji wirnika. Wzrost wibracji związany jest z odbieraniem części energii mechanicznej z wirnika niezbędnej dla podtrzymania tych drgań. Odchylenie osi wirnika od osi geometrycznej komory powoduje, źe ustawienie części łopatek wirnika, znacznie odbiega od optymalnych warunków ich opływu przez strugę. Prowadzi to do zrywania ciągłości strugi za łopatkami, zmiany cyrkulacji cieczy wokół łopatek i wywołuje wzrost nierównomierności strugi w przekroju wlotowym do stoźka wylotowego. Im większa jest nierównomierność strugi to tym większe amplitudy drgań ciśnienia występują wzdłuź obwodu w przekroju wlotowym stoźka, a co za tym idzie tym większe drgania siły wymuszającej występują na wirniku.
Powstałe po przejściu przez łopatki wirnika turbiny zawirowania strugi, tworzą nowy wir spiralny lub osiowy (tzn. istniejący w osi wirnika), który powstaje po zejściu strugi wody z opływki. Jest on obserwowany w zakresie obciąźeń od N = 2MW do   N = 10 MW. Potwierdza to analiza trajektorii osi wału wirnika turbiny.
Naruszenie osiowości wiru (naruszenie współosiowego ustawienia opływki w komorze wirnika) prowadzi do powstawania silnych udarów w przestrzeni pod wirnikiem i pulsacji ciśnienia w stoźku wylotowym. Udary strugi przenoszą się na detale hydrozespołów, wywołują ich silną wibrację, co moźe doprowadzić np. do zerwania opływki wirnika, a nawet do odrywania koła wodnego od wału w rezultacie zmęczeniowego ścięcia szpilek. Jeźeli częstotliwość tych udarów jest bliska częstotliwości drgań własnych opływki (udary te mają charakter szumu) to mogą wywołać drgania rezonansowe opływki.

Aby zabezpieczyć się przed tymi udarami lub je minimalizować naleźy bezwzględnie zachować współosiowość wirnika i komory.

Załoźono, źe te właśnie udary spowodowały uszkodzenie opływki. Aby przekonać się o słuszności takiego załoźenia  przeprowadzono analizę drgań własnych opływki i wyniki porównano z analizą stanu wibracyjnego hydrozespołu.

Drgania własne opływki

Płaszczyzna I jest płaszczyzną, w której instalowane są szpilki montaźowe.

 2.1.2.2. Opływka nowa

Pomiar częstości drgań własnych opływki wykazał, źe drgania rezonansowe z dwoma średnicami węzłowymi mogą być wywołane wymuszeniami  o częstotliwości f = 38 Hz, f = 56 Hz i f = 113 Hz. Taka postać drgań własnych dominuje głównie w płaszczyżnie III, a amplitudy tych drgań zanikają w miarę zbliźania się do płaszczyzny pomiarowej I. W płaszczyżnie I występują drgania własne o częstości f = 228 Hz. Jednak jest to postać   z czterema średnicami węzłowymi o małej amplitudzie drgań. Składowa taka występuje w drganiach obudowy łoźyska turbiny i moźe być informacją o drganiach rezonansowych opływki w płaszczyżnie I eksploatowanego hydrozespołu.  Podczas analizy porównawczej drgań własnych opływki z drganiami pokrywy komory wirnika i obudowy łoźysk cały czas uwzględniano, źe dla przepływu turbulentnego - jaki jest w obecności warkocza wodnego, występuje duźa zgodność częstotliwości drgań własnych w wodzie i powietrzu.

Podsumowaniem prac było więc zalecenie, aby:

bezwzględnie zachować współosiowość komory i wirnika turbiny.

2.2. Przykład 2

Pomiary częstości drgań własnych podstawy pod łoźysko nośne.

   W jednej z elektrowni wodnej łoźysko wzdłuźne hydrozespołu spoczywa na podstawie noszącej w gwarze elektrownianej nazwę “stołek”. Stołek ten w kształcie dwóch połączonych znajdujących się jeden nad drugim pierścieni spoczywa na kratownicy generatora. Na stołku tym mocowane są podparcia segmentów nośnego łoźyska ślizgowego. W trakcie remontu stwierdzono, źe spawane połączenie obu pierścieni górnego i dolnego jest w wielu miejscach popękane. Pęknięte były spoiny łączące obie części. Przeprowadzono pomiary mające na celu wyznaczenie częstości drgań własnych stołka. Stołek został wzbudzony do drgań. Największa amplituda drgań wystąpiła przy wzbudzeniu siłą o częstotliwości f = 114 Hz. Były to drgania z dwoma średnicami węzłowymi. Okazuje się, źe połączenia spawane obu pierścieni były w miejscach występowania strzałek.
W badanym stołku dwa połączenia miały całkowicie popękane spoiny natomiast w pozostałych połączeniach jakie występowały w miejscach strzałek spoiny były częściowo naruszone. Naleźy zaznaczyć, źe przeprowadzone wcześniej pomiary pokazały, źe w drganiach pionowych obudowy łoźyska (mierzone na wannie olejowej) i w drganiach stojana dominuje składowa o częstotliwości f = 100 Hz. Składowa ta dominuje dopiero po wzbudzeniu generatora, podczas którego wirnik generatora przemieszcza się w inne miejsce niź te jakie zajmował w spoczynku i do jakiego powraca po zatrzymaniu hydrozespołu.    Strefa niebezpiecznych wymuszeń do drgań z uwagi na drgania własne “stołka” wynosi od f = 80 Hz do f = 137 Hz. W takim zakresie częstotliwości wymuszeń “stołek” będzie wzbudzany do drgań rezonansowych.
Celem poprawy tego stanu naleźy pierścienie połączyć poprzez umieszczenie spoin w węzłach drgań i wprowadzić tłumienie w strzałkach. Zaznacza się, źe “stołek” jest przykręcony do podstawy prawidłowo tzn. w miejscach występujących węzłów.

2.3. Przykład 3

Wyznaczenie częstości drgań własnych górnej kratownicy.

Podczas pierwszych uruchomień hydrozespołów w jednej z  elektrowni występowały stałe problemy z wywaźeniem wirników generatora. W związku z poszukiwaniem przyczyn tego stanu konstruktor generatora przeprowadził skrupulatne pomiary stanu dynamicznego hydrozespołu. Dokładne oględziny konstrukcji pozwoliły na podanie przez badających następującej informacji :..“gdy taki kołnierz (chodzi o tuleję prasowaną na stoźek wału) zdjęto z turbozespołu na stoźku wału zauwaźono ślady wskazujące na istnienie ruchu względnego pomiędzy kołnierzem i wałem. Pomiary wykazały, źe powierzchnia stoźka miała kształt lekko beczkowaty”...[3]. W tej sytuacji przeprowadzono pomiary, które miały na celu wyznaczenie częstości drgań własnych układu wsporczego łoźyska. Badania pozwoliły na stwierdzenie występowania czterech prędkości krytycznych : 320 [obr/min], 370 [obr/min], 700 [obr/min] i 766 [obr/min]. Ponadto na podstawie krzywych Nyquista stwierdzono, źe ...“krzywe wskazują na szybki wzrost drgań względnych wału przy zbliźaniu się do prędkości 600 [obr/min] (eksploatacyjnej)”... . Przeprowadzone impulsowe testy wibracyjne wskazały, źe częstotliwość drgań własnych wspornika górnego w osi elektrowni wynosi 10 Hz, a górnej części wirnika 10,1 Hz. Częstotliwość drgań własnych wspornika górnego w kierunku prostopadłym do osi hali wynosi 11,95 Hz. Wynika stąd, źe wirnik jak i górny wspornik mają wspólną częstość drgań własnych.
Poniewaź częstotliwość 10 Hz jest częstotliwością eksploatacyjną widać, źe wirnik jak i wspornik górny cały czas pracowały w strefie drgań rezonansowych. Prawdopodobnie to zjawisko spowodowało poluzowanie osadzenia tulei na wale generatora. Uzyskane wyniki pomiarów były podstawą do przeprowadzenia modernizacji konstrukcji wsporczej łoźyska nośnego polegającej na usztywnieniu obu górnych wsporników. 

2.4. Przykład 4.

Propagacja drgań rezonansowych.

 Po awarii nasypu ziemnego w jednej z elektrowni i po jej powtórnym uruchomieniu okazało się, źe na jednym z pośród trzech przebadanych hydrozespołów na obudowie uszczelnienia wału w komorze wirnika pojawia się składowa o częstotliwości f = 130 Hz. Składowa ta wcześniej nie występowała. Z uwagi na to, źe jej wartość nie jest duźa w porównaniu z innymi występującymi składowymi nie została ona odnotowana jako wielkość charakterystyczna. Równieź próba jej identyfikacji nie powiodła się. Na występowanie podobnej składowej zwrócił uwagę zespół pomiarowy badający zachowanie się gruntu wokół odtworzonej skarpy elektrowni. Tam juź składowa ta była na tyle dominującą, źe zainteresowała badających dynamikę gruntu. Nie udało się jednak znależć żródła jej pochodzenia. Kilka miesięcy po tym zdarzeniu na zlecenie ESP wyznaczano podstawowe częstości i postacie drgań własnych głównych elementów Hydrozespołu 2. W czasie wyznaczania częstości i postaci drgań własnych badano odcinek rurociągu wody doprowadzającej znajdujący się w dostępnej do badań sztolni. Po wzbudzeniu do drgań okazało się, źe spośród bardzo bogatego spektrum uzyskanych postaci drgań własnych jedną z dominujących postaci drgań z dwoma średnicami węzłowymi są drgania o częstotliwośc i f = 129,5 Hz i z trzema średnicami węzłowymi  o częstotliwości f = 139 Hz. Występujące drgania miały bardzo duźą amplitudę i jest wielce prawdopodobne, źe jedna z tych składowych była  obserwowana zarówno w uszczelnieniu wału jak i drganiach gruntu. Świadczyć to moźe o tym, źe badany odcinek rurociągu cały czas pracuje w strefie drgań rezonansowych co w skali czasu moźe być zjawiskiem niebezpiecznym zarówno dla gruntu jak i dla konstrukcji rurociągu. Pozostałe składowe miały częstotliwości znacznie większe od f = 230 Hz. Gdyby podczas pomiarów drgań gruntu znana była wartość częstości drgań rezonansowych moźna by było wykorzystując np. analizę korelacyjną przeprowadzić ocenę wpływu drgań rurociągu na drgania gruntu. Moźna z duźym prawdopodobieństwem przypuszczać, źe analiza taka byłaby przeprowadzona podczas badań drgań gruntu. Badania takie prowadzi się w celu optymalnego doboru przestrzeni pod rozbudowę zakładów przemysłowych. Chodzi tu o badanie wpływu rozchodzenia się drgań w aspekcie właściwej lokalizacji przyszłego posadowienia urządzeń itp.

3. Podstawowe częstości drgań własnych

 Z przytoczonych przykładów widać, źe dla kontroli stanu technicznego hydrozespołów i zwiększenia ich niezawodności naleźy koniecznie znać częstości i charakterystyczne podstawowe postacie drgań własnych następujących węzłów hydrozespołu:

• kratownicy nośnej generatora lub silnika,
• promieniowe, styczne - skrętne korpusu stojana generatora lub silnika,
• pokrywy komory wirnika pompy lub turbiny,
• łopatek aparatu kierowniczego, koła wodnego i wirnika przepływu osiowego,
• drgania skrętne dolnej obręczy koła wodnego wirnika o promieniowo osiowym przepływie,
• wału zespołu - giętne , skrętne, wahadłowe,
• nadstawki wału - wał wzbudnicy,
• rurociągu dolotowego,
• drgania własne fundamentu generatora lub silnika,
• innych węzłów konstrukcyjnych. 

Zaznacza się, ze znajomość postaci drgań własnych ułatwia niejednokrotnie montaź i w wielu przypadkach poprawia warunki bezpiecznej eksploatacji. W takim przypadku jako punkty połączeń naleźy wybierać miejsca występowania węzłów pozostawiając strzałki swobodne lub wykorzystując je dla skuteczniejszego rozpraszania energii drgań (np. montaź drutów tłumiących w łopatkach wirników turbin cieplnych).Naleźy zauwaźyć, źe częstość drgań własnych w róźnych kierunkach jest róźna i głównie zaleźy od sztywności konstrukcji w danym kierunku. Na przykład w kierunku poziomym w poprzek łapy kratownica jest bardziej podatna (mniejsza sztywność) niź w kierunku wzdłuź osi łapy. Zatem i częstość drgań własnych kratownicy w kierunku zgodnym z kierunkiem poprzecznym będzie mniejsza aniźeli częstość drgań własnych w kierunku zgodnym z kierunkiem wzdłuź łapy kratownicy. Dla kratownicy generatora częstość drgań własnych w kierunku pionowym moźe być w przybliźeniu określona na podstawie znajomości pomierzonego ugięcia statycznego [4]:

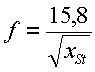Częstości pionowych drgań własnych kratownic wsporczych leźą zazwyczaj zakresie od f = 12 Hz do f = 40 Hz [5]. Wyjątkiem jest tu kratownica nośna hydrozespołów w EW Porąbka-Źar, dla których wyznaczona doświadczalnie częstość drgań pionowych wynosi wg. wytwórcy f = 7,5 Hz a wg innych pomiarów f = 5,6 Hz.
Częstości promieniowych drgań własnych korpusu stojana generatora wahają się w granicach od f = 50 Hz do f = 150 Hz. Częstości drgań skrętnych własnych korpusu stojana generatora wynoszą od f = 30 Hz do f = 80 Hz.
W hydrozespołach, w których czop oporowy oparty jest na pokrywie turbiny częstość drgań własnych pokrywy określa się na podstawie jej ugięcia pod wpływem masy części wirujących. Zazwyczaj dla turbin duźej mocy częstość ta równa jest od f = 40 Hz do f = 65 Hz, a dla turbin małych dochodzi ona do wartości od f = 80 Hz do f = 120 Hz.
Przy asymetrycznym dopływie cieczy do wirnika [6] naleźy liczyć się z moźliwością dwukrotnego wzrostu częstotliwości siły wymuszającej. Dlatego naleźy koniecznie wyznaczać częstotliwość wymuszenia i porównywać ją z częstotliwością drgań własnych łopatek. Częstotliwości drgań własnych powinny być wyznaczane eksperymentalnie. Rozwaźać naleźy tą postać drgań własnych dla, której występuje największa wartość amplitud drgań rezonansowych. Zazwyczaj mniejsza niź 4 - ta krotność. To samo dotyczy łopat kierownicy i korpusu komory wirnika. Pierwsza najbardziej niebezpieczna i powodująca często pęknięcia postać częstości drgań własnych łopatek turbin Kaplana zawiera się głównie w przedziale od 60 Hz do 120 Hz.
W promieniowo osiowych turbinach niebezpieczne są drgania skrętne dolnej obręczy jako masy podwieszonej na spręźystych płaszczyznach (łopatkach). Wg badań częstości te wynoszą od f = 40 Hz do f = 80 Hz [5].
Częstość poprzecznych drgań giętnych wału wahają się w granicach od f = 6 Hz do f = 20 Hz.
Częstość drgań skrętnych wału  określa się zazwyczaj na drodze obliczeniowej. Wartości częstości własnych drgań skrętnych zawierają się w granicach od f = 5 Hz do f = 40 Hz. Częstości drgań własnych wahadłowych wynoszą od f = 2 Hz do f = 8 Hz.
Częstości drgań własnych rurociągu dolotowego muszą być kaźdorazowo wyznaczane eksperymentalnie. Musi być wyznaczona zarówno częstość drgań powłoki i jej postać jak i postać drgań całego ciągu rurociągu. Jest to bardzo waźne poniewaź jak stwierdzono doświadczalnie częstości drgań własnych są silnie uzaleźnione są od sztywności podparć.

4. Stan dynamiczny hydrozespołów w innych od załoźonych warunkach pracy w aspekcie drgań  rezonansowych.

Bibliografia.